Blogs

Bayesian v/s Frequentist Statistics

Anurag Gulati

03 Mar 2024 • 6 min read

Destination might be the same, but which route do we choose?

Introduction

In the intricate world of statistics, it's akin to navigating two distinct clubs with their unique vibes—welcome to the realms of frequentists and Bayesians. Starting your stats journey often involves joining the frequentists, and exploring classic techniques such as t-tests and ANOVA. Yet, as you delve deeper into the mystical realm of probability distributions and the Bayesian crew's concepts of prior and posterior probabilities, the game gets more intriguing.

In this blog, we'll unravel the basics of both clubs, highlighting their differences and even delving into Bayesian inference. Despite the ongoing debate over which club is superior, each has its strengths and limitations.

Let's kick things off with the frequentists, the pioneers since the early 1900s. Probability is at the heart of their game, helping them decipher the main stats of a study. The frequentist approach usually includes hypothesis tests, featuring the p-value that dictates whether to embrace or reject the null hypothesis. For instance, imagine you're on a mission to determine the average weight of a population. By repeatedly testing, you can validate whether the observed difference is genuinely significant using hypothesis testing and p-values. In the next section, let us understand how Bayesian statistics work and what is the fundamental approach.

Bayesian Statistics Approach

The Bayesian approach to statistics revolves around Bayes' theorem, a fundamental concept in probability theory. Bayes' theorem is expressed as follows:

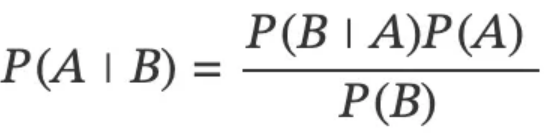
In simpler terms, it answers the question: If we already know that event B has occurred, what is the probability of event A? Without delving into the mathematical intricacies, the essence lies in understanding the relationships between posterior probability (P(A|B)), likelihood (P(B|A)), prior probability (P(A)), and marginal likelihood or evidence (P(B)).

💡

If you already learnt about the events during your hypothesis, then you would want to adjust your learnings and accordingly act. That is how the bayesian approach is fundamentally different from frequentist approach. Frequentist approach is based on a fixed hypothesis, formula. We will discuss about that in the below section.

How is Bayes' theorem related to an entire approach for statistics? Well, to answer that, lets dig into further interpretation of the formula above.

P(A|B) = posterior probability of some event

P(B|A) = likelihood of something happening

P(A) = prior probability

P(B) = marginal likelihood or evidence

💡

In light of the new evidence, the prior probabilities are updated and through likelihood, the posterior probabilities are generated. As you know that every event in the world is "uncertain". Bayesian approach likes to preserve this uncertainty by updating the evidence constantly as it becomes available.

So to summarize, Bayes’ idea is:

Initial belief + New Information = New belief

Therefore, Prior probability + New Evidence = Posterior probability

Contrasting this with the frequentist approach, which focuses on creating hypotheses, collecting sample data, and confirming or refuting hypotheses based on collected evidence, the Bayesian approach takes a different route. While the frequentist method works well for events with ample historical data, it may falter when faced with situations like a first-time election in a country. In such cases, where data is limited, the Bayesian approach excels as it embraces uncertainty and dynamically adjusts results as new evidence emerges. In essence, Bayesian statistics become particularly valuable when dealing with events characterized by sparse or evolving data.

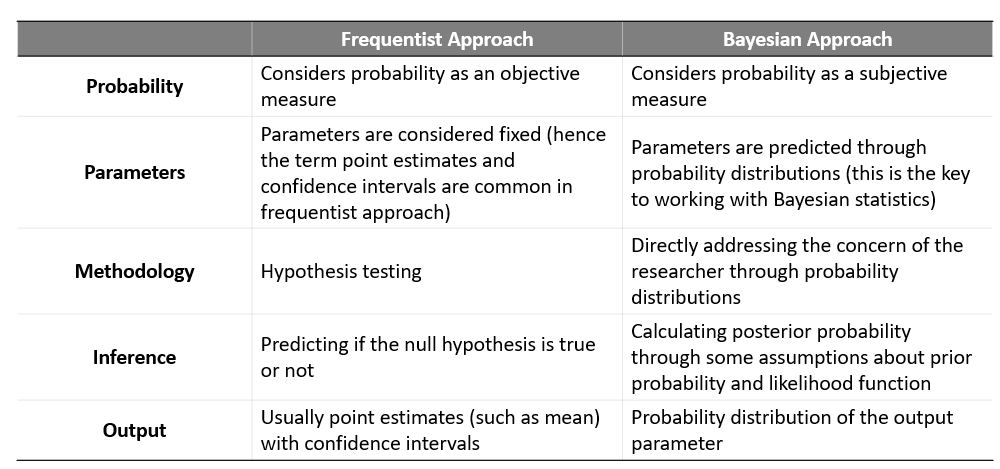
Differences between frequentist vs Bayesian approach

Below are some differences in frequentist v/s Bayesian approach for statistics:

Interpretation of Bayesian Approach

Consider a scenario where a patient receives a positive diagnosis for a specific disease. The natural question arises: What are the chances that the individual actually has the disease, given the positive test result? Enter Bayes' theorem to the rescue. The crucial aspect here is establishing or calculating the prior probability. If the disease is rare, the initial probability of someone having the rare disease would be low. Subsequently, more data is gathered to determine the likelihood of obtaining a false positive result when dealing with a rare disease. All these components come together to calculate the posterior probability, essentially representing new beliefs post the acquisition of additional evidence. The subjective nature of this process mirrors how humans, often unknowingly, apply Bayesian reasoning in everyday life. We continuously gather evidence, update our beliefs, and shape new perceptions—an implicit application of Bayesian principles.

In real-world applications, the complexity surpasses the simplicity of the aforementioned example. However, the underlying principles remain intact. To address more intricate problems using the Bayesian approach, the initial step involves calculating a prior probability. Notably, in contrast to a "static" probability, the Bayesian perspective often deals with probability distributions. Data serves as the catalyst to generate new evidence, subsequently updating posterior beliefs, which, in real-world scenarios, manifest as updated probability distributions. It's crucial to note that Bayesian problem-solving doesn't yield a single static number; instead, it produces a probability distribution. Point estimates (or static numbers in the form of averages), if needed, are then derived from these probability distributions, providing a more comprehensive and nuanced understanding of the underlying uncertainties.

Limitations of Bayesian approach

A) The selection of a prior in Bayesian analysis is inherently subjective, introducing a level of complexity driven by the need to make certain assumptions. The definition and choice of the prior event play a pivotal role in shaping the Bayesian algorithm. Without a well-defined prior event, the Bayesian approach may lack meaningful significance.

B) From a computational standpoint, the Bayesian approach can be computationally intensive, especially when dealing with extensive data sets and the computation of probability distribution curves to derive parameters. In some instances, the computational burden of Bayesian methods contrasts with the relatively simpler approach of frequentist methods, making the latter a more straightforward choice for reaching conclusions in certain scenarios.

Bonus Section - where did I get the idea for this blog?

Well, let me directly show you. I was sipping a hot cup of tea on the weekend when I saw two exactly similar cups with same amount of tea. I thought that just like these two cups, which are looking similar from the outside, might be so different if we look closely on the outside and the inside. They might even have been made through different processes (which is not visible at face value). Similarly, the two statistical approaches sometimes might produce same results, however, are fundamentally different to the core.

References: